CHAPTER 1 – Preface
CHAPTER 2 – Electricity: What It Is and How It Works.
- 2-1 Electricity – A Brief Summation of How Electricity Works.
- 2-2 Current, Voltage, and Resistance – The Three Components of Electricity.
- 2-2.1 Current
- 2-2.2 Voltage
- 2-2.3 Resistance
- 2-3 Ohm’s Law – The Mathematical Relationship Between the Three Components of Electricity.
CHAPTER 3 – Circuits and Basic Circuit Components.
- 3-1 Circuits – A Discussion of the Three Basic Types of Circuits.
- 3-1.1 Series circuits
- 3-1.2 Parallel circuits
- 3-1.3 Series-parallel circuits
- 3-2 Basic Components of an Electrical Circuit.
- 3-2.1 The electrical power source
- 3-2.2 The load
- 3-2.3 The wiring or conductive path
- 3-2.4 The controls
- 3-2.5 General circuit diagnostic
CHAPTER 1 – PREFACE
In the first two sections of this school, we did an in-depth study of general hydraulic theory. In this section, we will discuss the theory and fundamentals of DC electricity as it pertains to HWH equipment.
There are two theories of how current flows through a circuit, the Electron Theory and the Conventional Theory. The Electron Theory says that current flows from the negative side to the positive side. Section 2 does show that the electrons flow from negative to positive but the Conventional Theory says current flows from the positive side to the negative side. Except for section 2.1, we will work off of the Conventional Theory of current flow, positive to negative.
CHAPTER 2 – ELECTRICITY: WHAT IT IS AND HOW IT WORKS
2-1 Electricity – A Brief Summation of How Electricity Works
ELECTRICITY is the flow of electrons from atom to atom in a conductor. Atoms are made up of three particles, electrons (- or negative charge), protons (+ or positive charge) and neutrons (neutral charge). The protons and neutrons are the core of the atom and the electrons are in rings that orbit around the core. The positive charge of the protons attracts the negative charge of the electrons which keeps them in their rings around the core of the atom. Each atom of the same element has an equal number of electrons and protons so in a normal state, an atom is electrically neutral. The number of neutrons in an element is not necessarily the same as the number of electrons and protons in that element.
The rule that makes electricity work is “like charges repel and unlike charges attract”. When some force such as friction causes an electron to leave the outer ring of the atom, it changes the charge state of the atom. The atom gaining an electron becomes negatively charged and the atom that loses an electron becomes positively charged. When a conductor such as a copper wire has a positive charge at one end and a negative charge at the other, the electrons in the conductor will start moving. The positive charge at the end of the conductor will attract an electron (a negative charge) from an atom. That atom will then attract an electron from a neighboring atom leaving that atom positively charged. That atom then attracts an electron and so on and so on with billions and billions of atoms. The electrons flow through the conductor from the negatively charged end to the positively charged end. Now you have electricity.

The plus charge attracts an electron which leaves a hole in the outer ring of the atom. The atom is now positively charged.

The process is now started and as an electron is pulled from one atom, the charge state of that atom changes and it pulls an electron from another atom. The flow of the electrons is electricity.
2-2 Current, Voltage and Resistance – The Three Components of Electricity
CURRENT, VOLTAGE AND RESISTANCE: Although possibly interesting to some, the previous discussion has absolutely nothing to do with learning to diagnose an electrical issue. The following discussion will also have some useless but interesting facts. BUT this section is important to understand because we will talk about what makes electricity work.
There are three basic factors that we deal with when working with electricity. It is important to understand these to perform diagnostics on an electrical system. The three factors are Current, Voltage and Resistance.
2-2.1 Current is the flow of electrons through a conductor. Current is measured in amperes. The following is one of those useless facts. One ampere (from now on we will refer to amperes as amps) is a flow of 6.28 billion billion electrons moving past one point in one second. The number looks like this: 6,280,000,000,000,000,000. Current is the equivalent to flow, gallons per minute, in a hydraulic system.
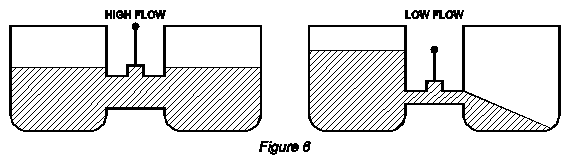
2-2.2 Voltage is the force or pressure that pushes the current through the circuit. Voltage is to an electrical circuit as pressure is to a hydraulic system. Without pressure fluid cannot flow through the hydraulic circuit. Without voltage, electrons will not move through the electrical circuit. Voltage is a Potential force. This means even if nothing is turned on, there can still be voltage. You can have voltage (pressure) without current (flow) but you cannot have current (flow) without the push of voltage (pressure). A good analogy would be a tank full of water connected to an empty tank through a tube with a closed valve.

The full tank has pressure in it from the weight of the water. The empty tank has no pressure. At the valve there is a potential force because there is pressure on one side of the valve and not the other. The full tank would be the negative side of a battery and the empty tank would be the positive side of the battery. Like the water tanks, voltage (the potential force) exists at the switch even though no electrons are moving. If the valve is opened, the water can flow from the full tank to the empty tank. The same thing happens if you close the switch that isolates the negative from the positive side of the battery. With the switch closed, excess electrons from the negative side can now flow to the positive side.

When the water level in the two tanks becomes equal, there will be no more flow because there is no differential of pressure to move the water. The potential force is gone. No pressure, no flow. The same thing happens as the battery discharges, that is, loses the potential energy that is voltage. There are no excess electrons to be attracted to the positive side, no difference in potential. No voltage, no current. See the figures on the next page.

2-2.3 Resistance is the opposition to the flow of electrical current. The unit of measurement for resistance is the ohm. All materials in an electric circuit create resistance, some more than others. Materials such as platinum, gold, silver and copper have a lower resistance value and are excellent conductors. Copper is the most common of the four to be used as a conductor due to the cost of the other three. Gold and silver are used as contacts in some relays and switches. Aluminum is also used as a conductor but has much more resistance than copper. Materials such as plastic and rubber are very poor conductors and are used as insulators because they prevent the flow of current.
We can use the two water tanks to explain resistance. If the two tanks are connected with a large tube, when the valve is opened the water will flow from the full tank to the empty tank quicker than two tanks connected with a small tube.
The same is true with electricity. A larger diameter copper conductor will have more electrons that can flow through the circuit than a small diameter copper conductor.

In hydraulics, there is a loss of pressure at the outlet end of a hose due to the friction between the fluid and the wall of the hose. The longer the hose, the more friction is introduced into the circuit, the greater the loss of pressure. Again, the same is true with electrical conductors or wires. The longer the wires, the more voltage loss there will be at the load. Some time ago, we did a test up in electrical engineering at HWH where we took a car battery and about 20 feet of 18 gauge wire and connected each end of the wire to one of the battery posts. Nothing happened, the wire did not even get hot (yes, the battery was fully charged).
If a wire is too long, there may not be enough voltage to push the current through. If the wire is to small a gauge, the voltage may try to push too much current through. This would create heat in the wire and if the wire is too small, it could possibly melt the wire. This is why wires are protected with fuses rated for the amount of current a wire can carry.
Another piece in an electrical circuit that creates resistance is the load. Light bulbs, a solenoid valve, a relay, an electronic piece of equipment such as a processor or a motor are all examples of a load in the circuit. The larger the load, the greater the resistance is in the circuit. Once again, the two water tanks can be used to represent the resistance a load creates in a circuit.

In the first example, we show a paddle wheel between the two tanks after the valve. With only the paddle wheel in the circuit, the load is small and creates little resistance. The water flows to the second tank with only a little interference. In the second example, we have attached a machine to the paddle wheel with a belt. Now the paddle wheel resists the flow of water as it tries to turn the machine. The machine has added resistance to the circuit and the water will not flow to the second tank as quickly as it did in the first example.
When the voltage in a circuit is constant, the total resistance in the circuit determines the current.
Resistance comes in many different forms besides the type, size, and length of the conductor(s) in the circuit or the size of the load(s) in the circuit. The connection points in the circuit (pin connectors, ring terminals, relay posts, etc.) are usually made from different materials than the wire so they would have a different resistance value. They could be brass, steel, stainless steel or tin coated copper, to name a few. The resistance created by good connection points will in most cases be negligible and could probably not be measured with an average voltmeter. Switch contacts and relay contacts can introduce resistance into the circuit, especially if they are pitted, arced or worn. The two main things in an electrical circuit that will create unwanted resistance that is not figured into the design of that circuit are loose connections and corrosion. A loose connection means that less material in the connection will be making contact. Like a smaller wire, the smaller amount of surface contact at the connection allows less current to flow through the connection. A loose connection is usually fairly simple to detect. Connections, whether they are soldiered, pin type, ring terminals or fast-on spade type connections should feel tight when you try to move them (just don’t use so much force you create a loose connection). Corrosion is the nasty little thing that can cause a lot of problems and is often overlooked or misdiagnosed. Corrosion is caused by the reaction of the metals in the circuit with air and/or water. Unlike metals can cause a corrosive connection. Contact between aluminum and steel can create devastating corrosion in an electrical circuit. Corrosion can add a very large amount of resistance to any electrical circuit. Even connections that do not appear to be corroded can have corrosion between the contact points of the connection that are not apparent with a simple visual inspection. Switch or relay contacts can be corroded. Wires and pc boards can also be corroded creating resistance. And don’t assume a “water proof” connector is not corroded. This is a common mistake I have seen: The pump motor doesn’t run so the pump relay is replaced. Now the pump motor runs. Was the relay really bad or when the wires were removed and attached to the new relay, was a bad connection or the corrosion factor removed?
But I get ahead of myself. It’s not time for diagnostics yet. It’s just that loose connections and corrosion which cause voltage problems are several of the most overlooked and misdiagnosed problems encountered and no matter how many times during this school we discuss it, it is probably not enough.
2-3 Ohm’s Law – The Mathematical Relationship Between the Three Components of Electricity.
OHM’S LAW is the mathematical relationship between the amount of voltage, current and resistance in an electrical circuit. A German physicist, Georg Simon Ohm, established this relationship in 1827. Ohm’s law is V (volts) = I (amps) X R (ohms or resistance). It takes one volt of pressure to move one amp of current against one ohm of resistance. The following triangle is an easy way to remember Ohm’s law and the three ways it can be written.
V = I X R | I = V ÷ R | R = V ÷ I

As long as you know two of the values in the circuit, you can figure the third value by using one of the above formulas that make up Ohm’s law. Under standing the relationship between voltage, current and resistance is important when diagnosing electrical issues, but you may never actually use the formulas of Ohm’s law when working on an electrical issue with an HWH system.
In electricity, power is measured in watts. The formula for figuring power or watts is W (watts/power) = V (volts) X I (current/amps). If you understand the relationships between volts, amps, ohms and watts, it is easier to understand how raising or lowering these values can affect a system. Later, we will use a few examples to show you how lowering voltage or increasing resistance changes how a system performs.
CHAPTER 3 – CIRCUITS and BASIC CIRCUIT COMPONENTS
3.1 Circuits – A Discussion of the Three Basic Types of Circuits
CIRCUITS: There are three types of electrical circuits, the series circuit, the parallel circuit and the series-parallel circuit. In the discussions of these circuits, we will refer to the resistors in the circuits but these could be any type of load in the circuit, not just a resistor.

3-1.1 Series circuits have only one path for current to flow along. All components in the circuit are connected end to end. Series circuits have the following features:
1. The total circuit resistance is the sum of all resistors in the circuit. (This would include wires, switches, connections and loads.)
2. The current through each resistor is the same.
3. The voltage drops across each resistor is different if the values of the resistors are different.
4. The sum of all the voltage drops in the system will be equal to the voltage source.
Below, we will show several examples of series circuits. We will also do the math to show circuit resistance, circuit current and voltage drops across the resistance.
Example 1: A series circuit with one 4 ohm resistor. | |
|
|
Example 2: A series circuit with one 2 ohm resistor, one 5 ohm resistor and one 3 ohm resistor. | |
|
|
3-1.2 Parallel circuits have multiple paths for current to flow. Each resistor in the circuit provides a separate path for current to flow. The resistors are side by side instead of end to end. Parallel circuits have the following features:
1. The voltage drop across each resistor is the same. It will be equal to the voltage source.
2. The current through each resistor will be different if the resistance values of the resistors in the circuit are different.
3. The total current in the circuit is the sum of the individual currents through each resistor.
We will again show several examples of a parallel circuit complete with the mathematics showing the different values in the circuit.
Example 1: A parallel circuit with a 2 ohm resistor and a 6 ohm resistor | |
|
|
Example 2: A parallel circuit with a 3 ohm resistor, a 4 ohm resistor and a 5 ohm resistor | |
|
|
3-1.3 Series-Parallel Circuits simply have a combination of the two circuits explained above. The circuit has one or more resistors in series with a parallel combination of resistors. Depending on the amount of resistors in the circuit that are in a parallel configuration, figuring circuit resistance or current and voltage drops can be fairly simple to very complex. I will give you some formulas and procedures for figuring values for a series-parallel circuit along with one example, but fortunately this is not something that will be important to remember or even to refer to when dealing with HWH® systems.
The way to work with this type of circuit is to first figure the total resistance of the parallel circuit then add that to the resistance of the resistor(s) that are in series with the parallel part of the circuit. For the example on the next page that would be R1 + total resistance of R2, R3 & R4. Once we do that, we can use I = V ÷ R to figure the total circuit current. This will let us let us figure the voltage drop across R1 and tell us what voltage is available for R’s 2, 3, and 4. Then we can figure the current for the individual resistors in the parallel circuit. The reason this is more difficult is because we don’t know the voltage for the parallel part of the circuit. We can’t use I = V ÷ R to figure the parallel circuit resistance as we did with the simple parallel circuit examples because we don’t know what V is. It’s a catch 22 problem. We can’t figure the resistance of the parallel circuit without knowing the voltage drops, but we can’t figure the voltage drops without knowing the resistance of the parallel circuit. This is where some new formulas come into play. The way to figure the total resistance of the parallel circuit is fairly simple. The formula for the example on the next page is as follows:
Total parallel circuit resistance =
1
1 + 1 + 1 or 1 ÷ [(1 ÷ R2) + (1 ÷ R3) + (1 ÷ R4)]
R2 R3 R4
If there were more resistors in the parallel circuit, you would just add more R’s to the above equation. There is a short cut for this problem if there are only 2 resistors in the parallel part of the circuit. That formula is: The total circuit resistance in a parallel circuit with 2 resistors is the product of the two resistors divided by the sum of the two resistors. Mathematically the formula would look like this:
Total parallel circuit resistance with 2 resistors = R X R or (R X R) ÷ (R + R)
R + R
This formula can be used on any parallel circuit with only two resistors.
Example: A series-parallel circuit has a 10 ohm resistor in series with a parallel group of resistors with values of 8 ohms, 4 ohms and 8 ohms. |
|
The total resistance of the parallel part of the circuit is 2 ohm. 1______ The total circuit current is 1 amp. The voltage drop for R1 is 10 volts. The current through R1 is 1 amp. The voltage drop for R2, R3 and R4 is 2 volts across each resistor. |
3-2 Basic Components of an Electrical Circuit
BASIC COMPONENTS OF AN ELECTRICAL CIRCUIT: There are four basic components to all electrical circuits, the electrical power source, the load, the wiring, and the controls.
3-2.1. The electrical power source. For nearly all HWH systems, the power source will be the battery system of the vehicle. Usually these will be 12 volt systems but some vehicles like the Prevost buses will have a 24 volt system. A large percent of motorized vehicles, especially in the RV industry, will have two separate battery systems. Towable units usually have just one battery system. On motorized vehicles, one system is referred to as the chassis or engine batteries and the other is referred to as the house batteries. In most cases the two systems will be the same voltage but again some vehicles like the Prevost bus may have two different voltage systems available. You are not going to run into too many 24 volt or combination 24/12 volt systems out there but it is important to remember it is possible. Using your 12 volt test light to check a leveling system on a Prevost could be expensive for you depending on what tool company you bought the test light from. Going either way will damage components or equipment but using 12 volt components or equipment on a 24 volt system will cause damage to the components or equipment in a VERY, short period of time. On motorized vehicles, the HWH control systems, light panels or control boxes, are connected to the chassis batteries through the ignition switch. When available, we prefer the use of the accessory side of the ignition switch. The loads for the system, such as the pump motor or valves, can be powered by either source. For towable units with just one battery system, it is recommended to use a master switch between the battery supply and the control system. This will eliminate any current draw on the batteries by the HWH system when it is not in use.
3-2.2. The load. The load is any component on the circuit that does some work such as a light bulb or LED, an electrically controlled valve, an electric relay, a processor, or the pump motor. Most of the loads in the circuit of an HWH system are a parallel circuit or a simple single load series circuit. The newer automatic systems do use a series circuit with two loads (hydraulic solenoid valves) in series. We will discuss this series circuit in more depth later in the school.

3-2.3. The wiring or conductive path. All the components of the electrical circuit have to be connected. This is accomplished with wires or in the case of printed circuit boards, the traces on the boards. The traces on a pc (printed circuit) board connect the components on the board like wires connect the parts of the system. The gauge (diameter) of the wire being used must be large enough to handle the maximum current the load can use and be able to maintain the voltage needed to operate the load. For example, the resistance of a coil in a large solenoid valve is approximately 1.2 ohms. With 12 volts to the valve, the valve will draw about 10 amps. The gauge of wire needed has to be capable of handling 10 amps. But you need to remember the longer the wire, the more resistance the wire adds to the circuit. A longer wire will cause a larger voltage drop. A 14 ga. wire will in most cases handle the load of a solenoid valve. If the length of the wires was extremely long, a larger gauge wire may be needed to reduce the voltage drop even though the smaller gauge wire will handle the maximum current the load may use.
Maybe the most important thing to remember about wiring or conductive paths that is the most likely thing to be overlooked is; the ground path for the circuit needs to be the same size or have the same capability as the positive side of the circuit. If the positive side of the circuit needs to be a 2 ga. wire, the conductive capability of the ground side needs to be equal to a 2 ga. wire, whether the conductive path is a wire or a mounting plate or bracket such as for our pump motors. This is true whether dealing with the battery cables or mounting location and brackets for the pump motor; or the smaller wires that supply ignition power to the control box.
3-2.4. The controls. The controls direct or regulate voltage and current to do work such as run a motor, shift a valve or turn on a light. The controls in a circuit can be very simple such as a fuse or the toggle switch used to operate the pump motor on a lever controlled, hand pump landing gear system or more complex like the control box for a 625 series automatic leveling system.
Switches come in many styles. There are manual switches such as toggle switches, rocker switches, key operated switches and push button switches. We even use something similar to a knife switch in the joystick valve to supply a ground path to operate the pump relay. There are electrically controlled switches such as relays. Relays are used in control boxes and on the pump assemblies. Relays have an electric coil that causes contacts in the relay to open or close. There are also electronic switches which are called transistors. Often, we use two or more circuits to perform a function. An example would be a joystick leveling system. When pushed to operate the jacks, the joystick lever completes a ground path for the coil of the pump relay. When activated, the contacts of the pump relay supply voltage and current to the pump motor from the battery. In this case, the pump relay acts as both a load and a switch. A computerized system will have two relays to activate the pump motor. There are three circuits used in this operation not counting the control panel to the control box.
These are simplified drawings of the joystick pump operation circuit and an automatic pump operation circuit.

There are many types of electronic components used in our systems that would be considered controls. These include diodes, resistors, capacitors and processor chips to name a few. These components are used to store, regulate, and direct voltage. Normally these components are used on light plates, control panels and in control boxes and are not considered when diagnosing problems in the field. We don’t recommend nor is it necessary in most cases to do diagnostics at the board level in the field. We will discuss some of these components in greater detail later in this school.
3-2.5 General circuit diagnostics. One of the meanings of the word “circuit” in the dictionary is “a closed, circular curve”. The easy way to say this is “a circuit is a circle”. For an electrical circuit to function, the circle must be complete. Any break in the circle will cause the circuit to not function.
Switches or other controls are used to complete the circle so the circuit can function. An open switch creates a break in the circle. Switches or other controls are designed into circuits to create an intentional break in the circuit to turn the load on and off. The problem is when unwanted breaks in the circle happen. The unwanted break could be a broken wire, a bad connection, a switch (control) problem, blown fuse, a malfunction of the load or a problem with the source (battery). Like with hydraulics, using the process of elimination is the best way to do diagnostics. Using wiring diagrams or schematics, list all the components of the circuit. Then, starting from one end, test and eliminate each component until the “break” in the circuit is found. For the drawing below the process would be as follows:
- Do you have + power and ground at the source? Yes.
- Do you have power to the switch? Yes.
- Do you have power through the switch? Yes.
- Do you have power to the load? Yes.
- Do you have ground to the load? No. The problem is between the load and the ground side of the source.
- Does the load function? You would only ask this question if the answers to the above five questions were yes.

When your testing produces a “no” answer to one of the above questions, you have isolated the problem. You could also start this process at the load but if you start anywhere else in the circuit, it is hard to eliminate things and the possibility of missing something increases. With the above circuit, the no answer was to the fifth question, “Do you have ground to the load?” Because there is power and ground at the source, and power to the load but no ground for the load, the break is in the connections or wiring between the source and the load. Admittedly, finding a break in a wire can be a headache, but the connections can be easily checked and then just run a new wire if that would be easier than trying to find a bad spot in the wire.
Almost all HWH® electrical systems can be treated in this manner. All you have to do is identify all the components that are part of the problem “circle”. Then eliminate them one at a time until the problem is isolated.
Click on “Download” for a test that will cover a little of everything that was discussed in this school. Download the test and email it to school@hwh.com we will correct it and send it back to you.





